[자료구조와 알고리즘] Algorithm Intermediate
2022. 6. 13. 17:20ㆍAI/Codestates
728x90
반응형
분할정복을 활용한 알고리즘
▶ 분할 정복 ( Divide and Conquer )
- 복잡하거나 큰 문제를 여러 개로 나눠서 푸는 방법
- 재귀호출은 같은 함수코드를 재호출하는 것 ( 같은 함수코드 사용 )
- 분할정복은 비슷한 작업을 재진행하는 것 ( 같은 함수코드는 아닐 수 있음 )
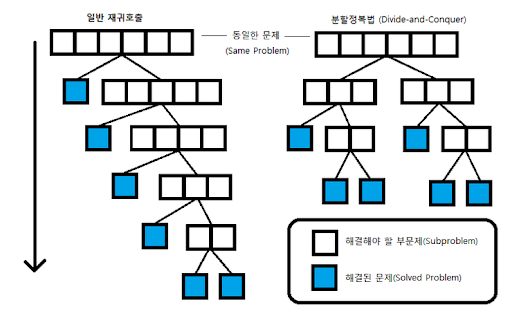
■ 분할정복의 과정
- 본 문제를 서브문제로 분할 ( Divide )
- 서브문제의 답을 구한 경우, 해당 답을 본 문제에 대한 답이 되도록 병합함 ( Merge )
- 문제를 분할할 수 없거나, 할 필요없는 경우에 대한 답을 구함 ( Base case, 기본 케이스 )
■ 분할정복의 조건
- 본 문제를 서브문제로 분할할 수 있는가? ( Divide )
- 서브문제의 답을 병합 ( 또는 조합 ) 하여 본 문제의 답을 구하는 것이 효율적인가? ( Merge, Conquer )
퀵정렬과 병합정렬 ( Quick Sort and Merge Sort )
▶ 퀵정렬 ( Quick Sort )
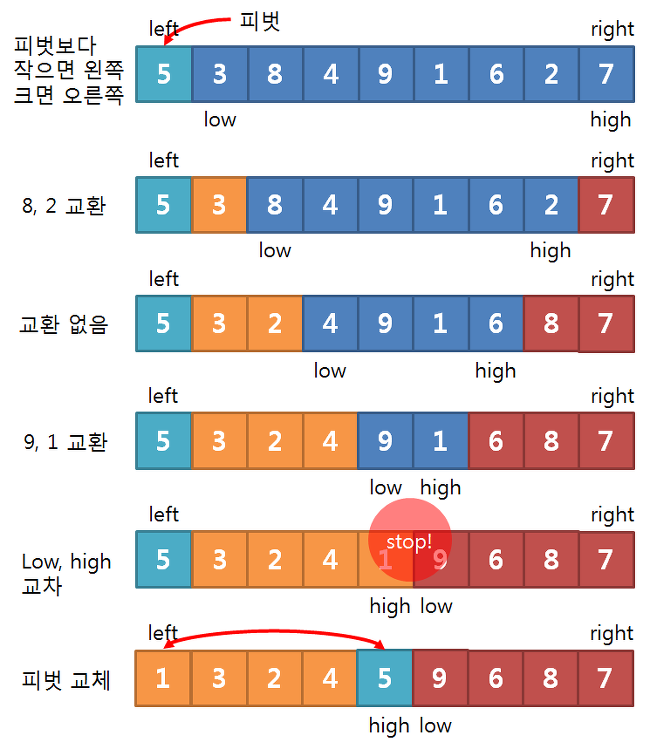
- 퀵정렬은 피벗이라는 별도의 노드를 지정해두고 재귀적으로 수행을 하기 때문에 통상적으로 병합정렬보다 더 빠름
- 한정적인 범위에서 데이터를 정렬하기 때문에 캐시를 덜 활용하고, 하드웨어적으로 효율적임
- 퀵정렬은 성능이 우수함에도 성능 편차가 크고, 피벗 ( 노드 ) 설정 등의 다루기 어려운 점이 존재하기 때문에 실무에서 활용되기가 어려움
- 최선의 시간복잡도 : O(nlogn)
- 최악의 시간복잡도 : O(n^2)
def quick_sort(li):
length = len(li)
if length <= 1:
return li
else:
pivot = li[0]
greater = [a for a in li[1:] if a > pivot]
lesser = [a for a in li[1:] if a <= pivot]
return quick_sort(lesser) + [pivot] + quick_sort(greater)▶ 병합정렬 ( Merge Sort )
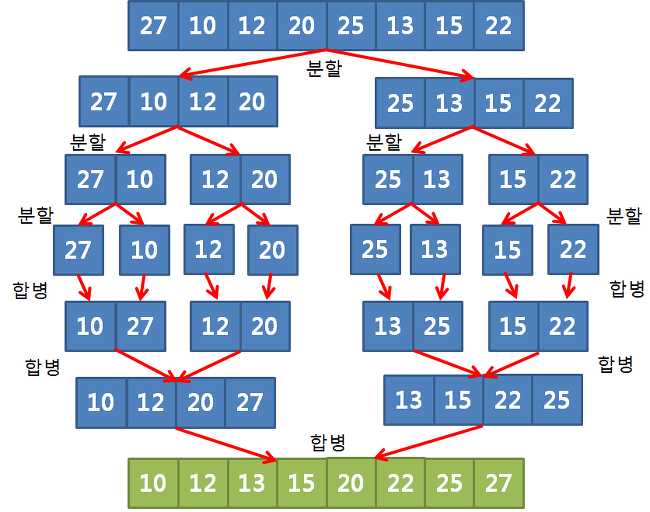
- 병합 정렬은 전체 데이터를 기준으로 처음과 끝을 계속해서 탐색하기 때문에 퀵정렬에 비해 느림
- 퀵정렬보다 빠르지는 않지만, 안정 정렬이기 때문에 데이터가 중복되었더라도 영향을 덜 받기 때문임
- 시간복잡도 : O(nlogn)
def merge(left, right):
answer = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
answer.append(left[i])
i += 1
else:
answer.append(right[j])
j += 1
answer.extend(left[i:])
answer.extend(right[j:])
return answer
def merge_sort(li):
length = len(li)
if length == 1:
return li
mid = length // 2
left = merge_sort(li[:mid])
right = merge_sort(li[mid:])
return merge(left, right)728x90
반응형
'AI > Codestates' 카테고리의 다른 글
| [자료구조와 알고리즘] Graph (0) | 2022.06.16 |
|---|---|
| [자료구조와 알고리즘] Hash Table (0) | 2022.06.15 |
| [자료구조와 알고리즘] Algorithm Fundamental (0) | 2022.06.11 |
| [자료구조와 알고리즘] DataStrucure Intermediate (0) | 2022.06.09 |
| [자료구조와 알고리즘] DataStructure Fundamenta (0) | 2022.06.08 |