2022. 4. 28. 22:27ㆍAI/Codestates
신경망 학습이 이뤄지는 과정

① 가중치 및 활성화 함수 연산을 반복적으로 수행 → 순전파
② ①의 과정을 모든 층에서 반봇 후 출력층에서 계산된 값을 출력 → 순전파
③ 손실함수를 사용하여 예측 값과 실제 값의 차이를 계산 → 손실 계산
④ 경사하강법과 역전파를 통해 각 가중치를 갱신 → 역전파
⑤ 학습 중지 기준을 만족할 때 까지 ① ~ ④의 과정 반복
▶ 이 과정을 현재 하고 있는 코딩으로 비유하자면 코딩 ( 순전파 ), 디버깅 ( 손실 계산 ), 오류수정 ( 역전파 )
순전파 ( Forward Propagation ) 란?
입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서 값을 내보내는 과정
입력 신호 정보를 입력층으로 부터 출력층까지 전달하여 값을 출력하는 알고리즘
① 입력층 ( 혹은 이전 은닉층 ) 으로부터 신호를 전달받음
② 입력된 데이터에 가중치-편향 연산을 수행
③ 가중합을 통해 구해진 값은 활성화 함수를 통해 다음 층으로 전달
손실함수 ( Loss Function ) 란?
→ 순전파를 거쳐 출력된 값과 그 데이터의 타겟값을 손실 함수에 넣어 손실 ( Loss or Error )를 계산
→ 예를 들어 MSE ( Mean-Squared Error ), CEE ( Cross-Entropy Error ), 이진 분류 ( binary_crossentropy ),
다중분류 ( categorical_crossentropy, sparse_categorical_crossentropy ) 등
역전파 ( Backward Propagation ) 란?
→ 순전파와는 반대 방향으로 손실 ( Loss or Error ) 정보를 전달 해주는 과정
→ 구해진 손실 정보를 출력층으로부터 입력층까지 전달하여 각 가중치를 얼마나 업데이트 해야할 지를 구하는 알고리즘
→ 신경망은 매 반복마다 손실을 줄이는 방향으로 가중치를 업데이트하는데 이 때 가중치 수정 방향을 결정하는 것을 경사하강법이라고 함
→ 가중치를 갱신하기 위해 편미분과 연쇄 법칙 ( Chain Rule )이 사용됨

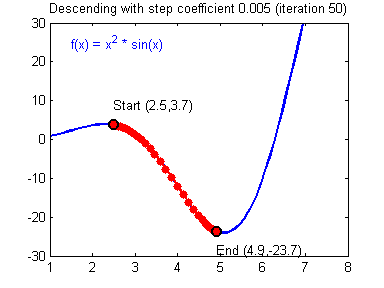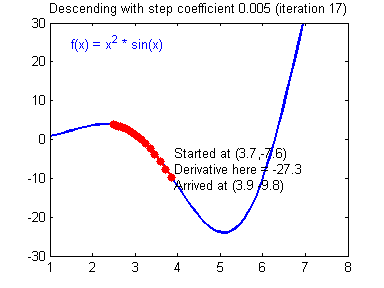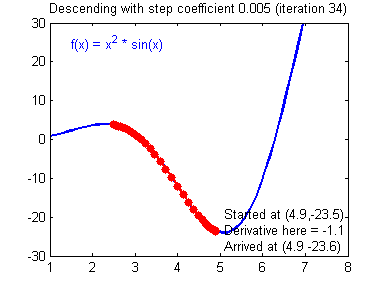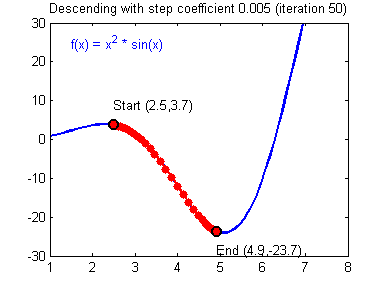
▶ 경사하강법 ( Gradient Descent, GD )

→ 손실 함수의 경사가 작아지는 방향으로 업데이트를 하면 손실 함수의 값을 줄일 수 있음
→ 매 Iteration 마다 해당 가중치에서의 비용 함수의 도함수 ( = 비용 함수를 미분한 함수 ) 를 계산 하여 경사가 작아질 수 있도록 가중치를 변경

■ 옵티마이저 ( Optimizer )
경사를 내려가는 방법을 결정

▶ 확률적 경사 하강법 ( Stochastic Gradient Desent, SGD )
전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력 후 손실 계산을 한 다음 역전파하여 가중치를 업데이트함
다시 말하면, Iteration 마다 1개의 데이터만 사용하게 됨 그렇기 때문에 가중치를 빠르게 업데이트 할 수 있다는 장점을 가짐
하지만 1개의 데이터만 보기 때문에 학습과정에서 불안정한 경사 하강을 보이게 되는 단점을 가짐

▶ 미니 배치 경사 하강법 ( Mini-Batch Gradient Desent )
위에 두 방법을 적절히 융화한 방법이 등장하게 되었음
N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 가중치를 업데이트함
즉, Iteration 마다 N개 ( = Batch Size )의 데이터를 사용하게 됨

■ 배치 사이즈 ( Batch Size )
일반적으로 배치 사이즈는 2의 배수로 설정하며, 메모리 크기가 허락한다면 큰 배치 사이즈를 쓰는 것이 학습을 안정적으로 진행 할 수 있음
데이터셋을 이루는 데이터의 수 ( # of Data ), Epoch, Batch Size, Iteration의 관계
데이터셋 전체를 몇 번이나 반복하여 학습할 지를 결정하는 Epochs
순전파-역전파 1회, 즉 가중치를 한 번 수정하는 단위를 Iteration
# of Data = Batch Size x Iteration
'AI > Codestates' 카테고리의 다른 글
| [Deep Learning] Hyperparameter Tuning (0) | 2022.05.02 |
|---|---|
| [Deep Learning] 더 나은 신경망 학습을 위한 방법들 (0) | 2022.04.29 |
| [Deep Learning] Artificial Neural Network (0) | 2022.04.27 |
| [Day 66] Section3 Review (0) | 2022.04.27 |
| [Day 60 ~ Day 65] Section 3 Project (0) | 2022.04.26 |