[Day 10] Sprint Review
2022. 2. 3. 16:33ㆍAI/Codestates
728x90
반응형
코딩부트캠프 | 코드스테이츠 - 비전공생도 개발자가 될 수 있습니다
코딩부트캠프를 찾는다면? 개발자로 커리어 전환을 위한 책임있는 코딩 교육 기관! 서비스 기획자, 그로스 마케터, 데이터 사이언티스트 등 다양한 전문 커리어에 도전하세요. 취업 성공의 후기
www.codestates.com
Summary
- 기술 통계치 ( Descriptive Statistics ) : 데이터를 설명하는 값 ( 혹은 통계치 )들
-
df.count() df.mean() df.std()
-
- 추리 통계치 ( Inferetial Statistics )
- ex) Population, Parameter, Statistic 등
- Effective Sampling
- Simple Randim Sampling : 모집단에서 Sampling을 무작위로 하는 방법
-
# Simple Random data = pd.DataFrame(np.random.randint(1,101,20), columns = ["samples"]) data
-
- Systematic Sampling : 모집단에서 Sampling을 할 때 규칙을 가지고 추출하는 방법
-
# systematic sampling (1~5까지 먼저 랜덤한 숫자 하나를 뽑고 5씩 늘여가는 규칙) samples = np.array(range(np.random.randint(1,5), 101, 5)) data_2 = pd.DataFrame(samples, columns = ["samples"]) data_2
-
- Stratified Random Sampling : 모집단을 미리 여러그룹으로 나누고, 그 그룹별로 무작위 추출을 수행하는 방법
-
# Stratified random sampling data = [i for i in range(1,101)] data_divided = [] data_list = [] # 1~10, 11~20 이런 형태로 10개의 그룹으로 나누기 for i in range(10): data_divided.append(data[0:10]) del data[0:10] # 그룹별로 2개씩 뽑아 data_list에 list형으로 저장 for j in data_divided: data_list.append(list(np.random.choice(j, 2))) # sum() 을 이용해 2차원 배열은 1차원 배열로 바꾼 후 DataFrame형으로 변환 data_3 = pd.DataFrame(sum(data_list, []), columns =["samples"]) data_3
-
- Cluster Sampling : 모집단을 미리 여러 그룹으로 나누고, 이후 특정 그룹을 무작위로 선택하는 방법
-
# cluster sampling data = np.arange(1,101) remain = np.random.randint(0,4) data_4 = pd.DataFrame(list(data[data % 5 == remain]), columns = ["samples"]) data_4
-
- Simple Randim Sampling : 모집단에서 Sampling을 무작위로 하는 방법
- 가설검증 : 주어진 상황에 대해서 하고자 하는 주장이 맞는지 아닌지를 판정하는 과정
- Student T - Test
- One Sample T - Test : 1개의 Sample 값들의 평균이 특정값과 동일한지 비교
-
from scipy import stats pv1 = stats.ttest_1samp(epop_tree, 400).pvalue
-
- Two Sample T - Test : 2개의 Sample 값들의 평균이 서로 동일한지 비교
-
from scipy import stats pv3 = stats.ttest_ind(zelkova_tree, kingcherry_tree).pvalue
-
- One Sample T - Test : 1개의 Sample 값들의 평균이 특정값과 동일한지 비교
- P - Value : 주어진 가설에 대해서 " 얼마나 근거가 있는지 " 에 대한 값으로 0과 1 사이의 값으로 Scale한 지표
- P - Value > 0.05 : 귀무가설을 기각하지 못한다. 귀무가설을 채택한다.
- P - Value <= 0.05 : 귀무가설을 기각. 즉, 대립가설을 채택한다.
- T - Test +
- 독립성 : 두 그룹이 연결되어 있는 ( Paired ) 쌍인지
- 정규성 : 데이터가 정규성을 나타나는지
- 등분산성 : 두 그룹이 어느정도 유사한 수준의 분산 값을 가지는지
- X^2 Test
- One Sample X^2 Test
-
from scipy.stats import chisquare chi1 = chisquare(df_sum, axis=None)
-
- Two Sample X^2 Test
-
from scipy.stats import chi2_contingency chi2_contingency(df)
-
- One Sample X^2 Test
- 자유도 ( Degrees Of Freedom ) : 해당 Parameter를 결정짓기 위한 독립적으로 정해질 수 있는 값의 수
- ANOVA ( One - Way ) : 2개 이상 그룹의 평균에 차이가 있는지를 가설검정하는 방법
-
from scipy.stats import f_oneway f_oneway(df_new['A'],df_new['B'],df_new['C'],df_new['D'])
-
- 1종 오류는 귀무가설이 실제로 참이지만, 이에 불구하고 귀무가설을 기각하는 오류이다. 즉, 실제 음성인 것을 양성으로 판정하는 경우이다. 거짓 양성 또는 알파 오류( α error )라고도 한다.
- 2종 오류는 귀무가설이 실제로 거짓이지만, 이에 불구하고 귀무가설을 채택하는 오류이다. 즉, 실제 양성인 것을 음성으로 판정하는 경우이다. 거짓 음성 또는 베타 오류( β error )라고도 한다.
- Many Samples
- 큰 수의 법칙 (Law Of Large Number ) : Sample 데이터의 수가 커질수록, Sample의 통계치는 점점 모집단의 모수와 같아진다.
-
#큰 수의 법칙 import numpy as np import pandas as pd pop = df_2['초미세먼지(㎍/㎥)'] large_numbers =[] for i in np.arange(5,740,5): s = np.random.choice(pop, i) large_numbers.append(s.var()) large_numbers mean_y = np.mean(large_numbers) (pd .DataFrame(large_numbers) .plot .line(color = '#343740') .axhline(y = mean_y, color = 'red') )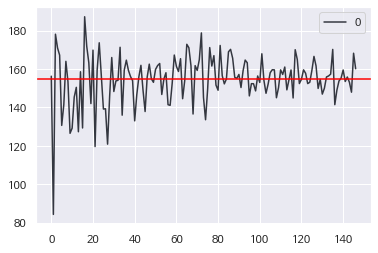
-
- 중심극한정리 ( Central Limit Teorem, CLT ) : Sample 데이터의 수가 많아질수록, Sample의 평균은 정규분포에 근사값으로 나타난다
-
#중심극한정리 import numpy as np import pandas as pd clt=[] pop = df_2['초미세먼지(㎍/㎥)'] size = [2, 10, 100, 500, 1000] for i in size: for j in np.arange(2,744,2): c = np.random.choice(pop,i) clt_mean = c.mean() clt.append(clt_mean) pd.DataFrame(clt).hist(color = '#698af5')




-
- 큰 수의 법칙 (Law Of Large Number ) : Sample 데이터의 수가 커질수록, Sample의 통계치는 점점 모집단의 모수와 같아진다.
- 신뢰도 : 신뢰도가 95%라는 의미는 표본을 100번 뽑았을 때 95번은 신뢰구간 내에 모집단의 평균이 포함된다.
- 이유불충분의 원리 ( = 무관심의 원칙, The Princilpe Of Insufficient Reason ) : 다른 사건보다는 하나의 사건을 기대할 만한 어떤 이유가 없는 경우에는 가능한 모든 사건에도 동일한 확률을 할당해야 한다는 원칙
- 총 확률의 법칙 ( The Raw Of Total Probability ) : A라는 특정 확률 변수에 대해, 모든 가능한 이벤트의 총 확률은 1이다.
- 조건부 확률 ( The Raw Of Conditional Probability ) : 주어진 사건이 일어났다는 가정 하에 다른 한 사건이 일어날 확률
- 베이지안 이론 ( Bayesian Theorem )
-
P(B) = P(B|A)*P(A) + P(B|notA)*P(notA) P(A|B) = P(B|A)*P(A) / P(B) # 베이지안 정리 P(A|B) = P(B|A)*P(A) / P(B|A)*P(A) + P(B|notA)*P(notA) - TPR ( = 민감도, True Positive Rate = True Accept Rate) : 1인 케이스에 대해 1로 잘 예측한 비율
- FPR ( = 1 - 특이도, False Positive Rate = False Accept Rate ) : 0인 케이스에 대해 1로 잘못 예측한 비율
-
728x90
반응형
'AI > Codestates' 카테고리의 다른 글
| [Day 12] Linear Algebra + (0) | 2022.02.07 |
|---|---|
| [Day 11] Vector / Matrix (0) | 2022.02.04 |
| [Day 9] Bayesian (0) | 2022.01.28 |
| [Day 8] Confidence Interval (0) | 2022.01.27 |
| [Day 7] Hypothesis Test 2 (0) | 2022.01.26 |